Ohmi seadus terve ahela ja ahela lõigu jaoks: valemi, kirjelduse ja selgituse kirjutamise võimalused

Professionaalsel elektrikul või elektroonikaspetsialistil pole võimalust oma tegevuses Ohmi seadusest mööda minna, lahendades elektroonika- ja elektriahelate seadistamise, reguleerimise ja remondiga seotud probleeme.

Tegelikult peavad kõik sellest seadusest aru saama. Sest elektriga tuleb igapäevaelus kokku puutuda.

Ja kuigi keskkooli õppekavas on saksa füüsiku Ohmi seadus ette nähtud, ei õpita seda praktikas alati õigeaegselt. Seetõttu käsitleme oma materjalis sellist eluks olulist teemat ja mõistame valemi kirjutamise võimalusi.

Üks sektsioon ja täielik elektriahel

Arvestades elektriahelat Ohmi seaduse rakendamise seisukohast vooluringile, tuleks märkida kaks võimalikku arvutusvõimalust: eraldi sektsiooni ja täisväärtusliku vooluahela jaoks.

Elektriahela sektsiooni voolutugevuse arvutamine

Elektriahela osa loetakse reeglina vooluringi osaks, mis välistab EMF-i allika, kuna sellel on täiendav sisetakistus.

Seetõttu näib arvutusvalem antud juhul lihtne:

I = U/R,

Kus vastavalt:

• I – voolutugevus;
• U – rakendatud pinge;
• R - vastupanu.

Valemi tõlgendamine on lihtne - vooluahela teatud osa läbiv vool on võrdeline sellele rakendatud pingega ja takistus on pöördvõrdeline.

Niinimetatud graafiline karikakra, mille kaudu esitatakse kogu Ohmi seadusel põhinevate formulatsioonide variatsioonide komplekt. Mugav tööriist taskus hoidmiseks: sektor “P” - võimsusvalemid; sektor “U” - pingevalemid; sektor “I” - kehtivad valemid; sektor “R” - takistusvalemid

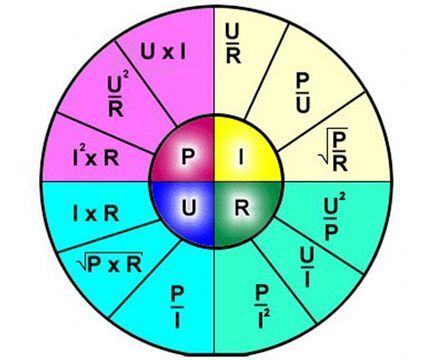
Seega kirjeldab valem selgelt elektriahela eraldi sektsiooni läbiva voolu sõltuvust teatud pinge ja takistuse väärtustest.

Valemit on mugav kasutada näiteks pinge ja voolutugevuse korral vooluringi joodetava takistuse parameetrite arvutamisel.

Ohmi seadus ja kaks tagajärge, mida peab teadma iga professionaalne elektromehaanikainsener, elektriinsener, elektroonikainsener ja igaüks, kes on seotud elektriahelate tööga. Vasakult paremale: 1 - voolu määramine; 2 - takistuse määramine; 3 - pinge määratlus, kus I - vool, U - pinge, R - takistus

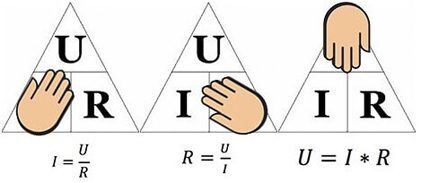
Ülaltoodud joonis aitab määrata näiteks voolu, mis voolab läbi 10-oomise takistuse, millele rakendatakse 12-voldine pinge. Väärtused asendades leiame – I = 12 / 10 = 1,2 amprit.

Sarnaselt lahendatakse takistuse (kui vool ja pinge on teada) või pinge (kui pinge ja vool on teada) leidmise probleemid.

Seega saate alati valida vajaliku tööpinge, vajaliku voolutugevuse ja optimaalse takistusliku elemendi.

Kasutamiseks kavandatud valem ei nõua pingeallika parameetritega arvestamist.Ahel, mis sisaldab näiteks akut, arvutatakse aga erineva valemi abil. Diagrammil: A – ampermeetri sisselülitamine; V – voltmeetri sisselülitamine.

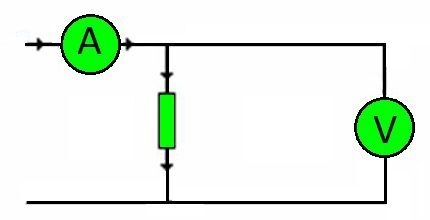
Muide, mis tahes vooluahela ühendusjuhtmed on takistused. Koormuse suurus, mida nad peavad kandma, määratakse pinge järgi.

Sellest lähtuvalt on jällegi Ohmi seadust kasutades võimalik sõltuvalt südamiku materjalist täpselt valida vajalik juhi ristlõige.

Meie veebisaidil on üksikasjalikud juhised kaabli ristlõike arvutamine võimsuse ja voolu poolest.

Arvutusvõimalus terve ahela jaoks

Täielik vooluahel koosneb sektsioonist (sektsioonidest) ja ka EMF-i allikast. See tähendab, et tegelikult lisatakse vooluahela sektsiooni olemasolevale takistuslikule komponendile EMF-i allika sisemine takistus.

Seetõttu on loogiline ülaltoodud valemit veidi muuta:

I = U / (R + r)

Loomulikult võib täieliku elektriahela Ohmi seaduse järgi EMF-i sisetakistuse väärtust pidada tühiseks, kuigi see takistuse väärtus sõltub suuresti EMF-i allika struktuurist.

Kuid keeruliste elektrooniliste ahelate, paljude juhtidega elektriahelate arvutamisel on oluline tegur täiendava takistuse olemasolu.

Arvutuste tegemisel täieliku elektriahela tingimustes võetakse alati arvesse EMF-i allika takistuslikku väärtust. See väärtus liidetakse elektriahela enda takistustakistusega. Diagrammil: I - vooluvool; R — väline takistuselement; r on EMF-i (energiaallika) takistustegur

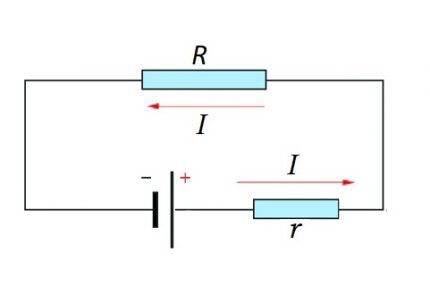
Nii ahela lõigu kui ka kogu vooluringi puhul tuleks arvestada loomuliku momendiga - konstantse või muutuva vooluga.

Kui ülaltoodud Ohmi seadusele iseloomulikke punkte vaadelda alalisvoolu kasutamise seisukohast, siis vastavalt vahelduvvoolule näeb kõik välja mõnevõrra erinev.

Seaduse mõju arvestamine muutuvale suurusele

Mõistet "takistus" läbiva vahelduvvoolu tingimuste suhtes tuleks pidada pigem "impedantsi" mõisteks. See viitab takistusliku koormuse (Ra) ja reaktiivtakisti koormuse (Rr) kombinatsioonile.

Selliseid nähtusi põhjustavad induktiivsete elementide parameetrid ja lülitusseadused muutuva pinge väärtuse - sinusoidse voolu väärtuse suhtes.

See on vahelduvvoolu elektriahela samaväärne ahel arvutamiseks Ohmi seaduse põhimõtetel põhinevate formulatsioonide abil: R - takistuskomponent; C on mahtuvuslik komponent; L — induktiivne komponent; EMF on energiaallikas; I - vooluvool

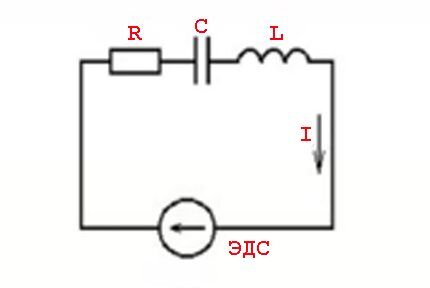
Teisisõnu, pinge väärtustest juhinduvad (lag) vooluväärtused, millega kaasneb aktiivse (takisti) ja reaktiivse (induktiivne või mahtuvuslik) võimsuse ilmumine.

Sellised nähtused arvutatakse järgmise valemi abil:

Z=U/I või Z = R + J* (X_L -X_C)

Kus: Z - impedants; R - aktiivne koormus; X_L , X_C – induktiivne ja mahtuvuslik koormus; J - koefitsient.

Elementide jada- ja paralleelühendus

Elektriahela elementide (ahela lõigu) puhul on iseloomulik punkt jada- või paralleelühendus.

Sellest lähtuvalt kaasneb iga ühenduse tüübiga erinev voolu ja pingevarustuse muster.Sellega seoses rakendatakse Ohmi seadust ka erinevalt, sõltuvalt elementide kaasamise võimalusest.

Jadaühendatud takistuselementide vooluahel

Jadaühenduse (kahe komponendiga ahela osa) puhul kasutatakse järgmist sõnastust:

• I = I₁ = I₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

See formulatsioon näitab selgelt, et olenemata järjestikku ühendatud takistuslike komponentide arvust, ei muutu vooluahela osa läbiva voolu väärtus.

Takistavate elementide ühendamine vooluahela sektsioonis üksteisega järjestikku. Sellel valikul on oma arvutusseadus. Diagrammil: I, I1, I2 - vooluvool; R1, R2 - takistuslikud elemendid; U, U1, U2 - rakendatud pinge

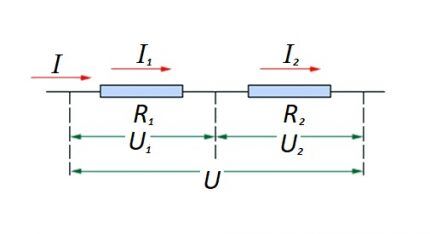
Ahela efektiivsetele takistuskomponentidele rakendatud pinge suurus on emf-allika väärtuse summa ja summa.

Sel juhul on iga üksiku komponendi pinge võrdne: Ux = I * Rx.

Kogutakistust tuleks pidada kõigi vooluahela takistuslike komponentide väärtuste summaks.

Paralleelselt ühendatud takistuselementide ahel

Takistuskomponentide paralleelse ühendamise korral peetakse järgmist sõnastust Saksa füüsiku Ohmi seaduse suhtes õiglaseks:

• I = I₁ +I₂ … ;
• U = U₁ = U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Paralleel- ja jadaühenduste kasutamisel ei ole välistatud võimalused "sega" tüüpi vooluringi sektsioonide loomiseks.

Takistavate elementide ühendamine vooluahela lõigul paralleelselt üksteisega. Selle variandi puhul rakendatakse teistsugust arvutusseadust. Diagrammil: I, I1, I2 - vooluvool; R1, R2 - takistuslikud elemendid; U on toitepinge; A, B - sisenemis-/väljapääsupunktid

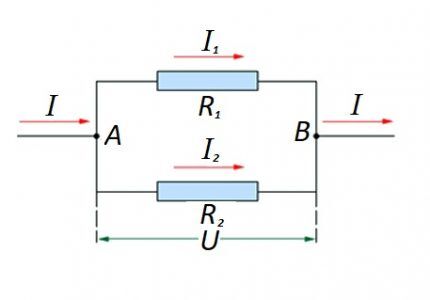
Selliste valikute puhul arvutatakse tavaliselt paralleelühenduse takistuse algväärtuse arvutamise teel. Seejärel lisatakse saadud tulemusele järjestikku ühendatud takisti väärtus.

Õiguse integraal- ja diferentsiaalvormid

Kõik ülaltoodud punktid koos arvutustega kehtivad tingimuste korral, kui elektriahelates kasutatakse nii-öelda homogeense struktuuriga juhte.

Samal ajal tuleb praktikas sageli tegeleda skeemide konstrueerimisega, kus juhtide struktuur erinevates sektsioonides muutub. Näiteks kasutatakse suurema ristlõikega või vastupidi väiksemaid juhtmeid, mis on valmistatud erinevatest materjalidest.

Selliste erinevuste arvessevõtmiseks on olemas nn diferentsiaalintegraal Ohmi seaduse variatsioon. Lõpmatu väikese juhi puhul arvutatakse voolutiheduse tase sõltuvalt pingest ja juhtivuse väärtusest.

Diferentsiaalarvutamiseks kasutatakse järgmist valemit: J = ό * E

Integraalarvutuse jaoks on sõnastus järgmine: I * R = φ1 – φ2 + έ

Need näited on aga pigem lähedasemad kõrgema matemaatika koolkonnale ja reaalses lihtsa elektriku praktikas neid tegelikult ei kasutata.

Järeldused ja kasulik video sellel teemal

Ohmi seaduse üksikasjalik analüüs allolevas videos aitab lõpuks teadmisi selles suunas kinnistada.

Ainulaadne videotund tugevdab kvalitatiivselt teoreetilist kirjalikku esitlust:

Elektriku töö või elektroonikainseneri tegevus on lahutamatult seotud hetkedega, mil tuleb reaalselt järgida Georg Ohmi seadust. Need on teatud tõepärasused, mida iga professionaal peaks teadma.

Laialdasi teadmisi selles küsimuses ei nõuta - piisab, kui õppida selgeks kolm peamist sõnastuse variatsiooni, et seda praktikas edukalt rakendada.

Kas soovite ülaltoodud materjali väärtuslike kommentaaridega täiendada või oma arvamust avaldada? Kirjutage kommentaarid artikli all olevasse plokki. Kui teil on küsimusi, küsige julgelt meie ekspertidelt.